ADMM¶
This document is devoted to the resolution of discrete mean field games via Augmented Lagrangian methods (see [BB00] for an example in fluid mechanics).
Packages¶
import numpy as np
from numpy import random
from mpl_toolkits import mplot3d
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import time
Potential formulation and dual minimization¶
We define a dual criterion
\[\mathcal{D}(P,u,\gamma) := \langle m_0(\cdot), u(0,\cdot)\rangle_{u} +\sum_{t\in \mathcal{T}} - F^\star[\gamma](t) \Delta_t\Delta_x- \phi^\star[P](t)\Delta_t - F^\star[\gamma](T)\Delta_x \]
and a dual problem
\[\begin{split}\begin{array}{c}
\displaystyle \sup_{\begin{subarray}{c}
(P,u) \in \mathcal{K}, \; \gamma\in \mathbb{R}(\bar{\mathcal{T}} \times S), \\
(a,b) \in \mathcal{Q}
\end{subarray}} \mathcal{D}(P,u,\gamma) \\
\text{s.t.} \begin{cases}
u(t,x)/\Delta_t - \gamma(t,x) = a(t,x) & (t,x) \in \mathcal{T} \times S,\\
-\alpha(t,x,y)P(t) -u(t+1,y)/\Delta_t = b(t,x,y) & (t,x,y) \in \mathcal{T} \times S \times S,\\
u(T,x)-\gamma(T,x) = 0 & x \in S,\\
\end{cases}
\end{array}\end{split}\]
where
\[\mathcal{K} = \mathbb{R}(\mathcal{T}) \times \mathbb{R}(\bar{\mathcal{T}} \times S), \qquad \mathcal{Q} := \left\{ (a,b) \in \mathbb{R}(\mathcal{T} \times S) \times \mathbb{R}(\mathcal{T} \times S \times S) , \quad \ell^\star[b](t,x) + a(t,x) \leq 0 \right\}.\]
Then we define the Lagrangian associated to the above problem:
\[\mathcal{L}(P,u,\gamma,a,b,m,w) = \mathcal{D}(P,u,\gamma) - \chi_{\mathcal{Q}}(a,b) - \langle m, (I_0/\Delta_t + I/\Delta_t + I_T)u - \gamma - \bar{a} \rangle_{m} - \langle w,-A^\star[P] -S^\star[u]/\Delta_t - b\rangle_{w}.\]
We define the Augmented Lagrangian parametrized by \(r>0\) as follows
\[\mathcal{L}_r(P,u,\gamma,a,b,m,w) = \mathcal{L}(P,u,\gamma,a,b,m,w) - \frac{r}{2}\| ((I_0/\Delta_t + I/\Delta_t + I_T)u - \gamma -\bar{a},-A^\star[P] -S^\star[u]/\Delta_t - b) \|^2_{m,w}.\]
Algorithm¶
The Algorithm is given by :
\((P^0,u^0,\gamma^0,a^0,b^0,m^0,w^0) \leftarrow (P,u,\gamma,a,b,m,w)\)
For \(0\leq n < N\)
Find
\[P^{n+1} \in argmax_{P \in \mathbb{R}(\mathcal{T})} \mathcal{L}_r(P,u^n,\gamma^n,a^n,b^n,m^n,w^n)\]
Find
\[u^{n+1} \in argmax_{u \in \mathbb{R}(\bar{\mathcal{T}} \times S)} \mathcal{L}_r(P^{n+1},u,\gamma^n,a^n,b^n,m^n,w^n)\]
Find
\[\gamma^{n+1} \in argmax_{\gamma \in \mathbb{R}(\bar{\mathcal{T}} \times S)} \mathcal{L}_r(P^{n+1},u^{n+1},\gamma,a^n,b^n,m^n,w^n)\]
Find
\[(a^{n+1},b^{n+1}) \in argmax_{(a,b) \in \mathcal{Q}} \mathcal{L}_r(P^{n+1},u^{n+1},\gamma^{n+1},a,b,m^n,w^n)\]
Actualise \((m,w)\) via a gradient descent step
\[(m^{n+1},w^{n+1}) = (m^{n},w^{n}) + q((I_0/\Delta_t + I/\Delta_t + I_T)u^{n+1}-\gamma^{n+1}-\bar{a}^{n+1}, - A^\star[P^{n+1}] - S^\star[u^{n+1}]/\Delta_t - b^{n+1})\]
End for
Return \((P^N,u^N,\gamma^N,a^N,b^N,m^N,w^N)\).
Data of the problem¶
def initial_mass(n):
m_bar = np.zeros(n)
for x in range(n):
m_bar[x] = np.exp(-(x-n/2)**2/(n/4)**2)
return(n*m_bar/np.sum(m_bar))
def displacement_cost(T,n):
dx=1/n
dt=1/T
disp = np.zeros((T-1,n,n))
for t in range(T-1):
for x in range(n):
for y in range(n):
disp[t,x,y] = ((y-x)*dx/dt)**2/4
return(disp)
def penalisation_congestion(T,n):
nu = np.zeros((T,n))
for t in range(T):
if t > T/2 and t < 3*T/4:
for x in range(n):
if x > n/2:
nu[t,x] = 10
return(nu)
def sharp_penalisation_congestion(T,n):
eta = np.zeros((T,n)) + 3
for t in range(T):
for x in range(n):
if (t > T/3 and t < 2*T/3) and (x > n/3 and x < 2*n/3):
eta[t,x] = 1/4
return(eta)
def reference_demand(T):
new_Db = np.zeros(T-1)
for t in range(T-1):
new_Db[t] = np.sin(t*(4*np.pi)/(T-1))
return(new_Db)
def alpha_cost(T,n):
dx=1/n
dt=1/T
disp = np.zeros((T-1,n,n))
for t in range(T-1):
for x in range(n):
for y in range(n):
disp[t,x,y] = (y-x)*dx/dt
return(disp)
def alpha_bar(alpha,T,n):
new_alpha = np.zeros((T-1,n))
a = np.zeros(T-1)
for t in range(T-1):
for x in range(n):
new_alpha[t,x] = np.sum(alpha[t,x]**2)
a[t] = np.sum(new_alpha[t])
return(a)
Computation of ADMM steps¶
Computation of \(P^{n+1}\)¶
Proximal formulation
\[\begin{split}
\begin{array}{rl}P^{n+1}& = \text{arg min}_{P \in \mathbb{R}(\mathcal{T})} \; \frac{r}{2} \| A^\star[P] + S^\star[u^n]/\Delta_t + b^n \|_{w}^2 + \phi^\star(P) \Delta_t - \langle w^n,A^\star[P] \rangle_{w}
\\
& = \text{arg min}_{P \in \mathbb{R}(\mathcal{T})} \; \frac{r}{2} \| A^\star[P] + S^\star[u^n]/\Delta_t + b^n \|^2 + \phi^\star(P)/ \Delta_x - \langle w^n,A^\star[P] \rangle \\
& = \text{arg min}_{P \in \mathbb{R}(\mathcal{T})} \; \frac{1}{2} \|P\|^2 + \langle P, A[S^\star[u^n]/\Delta_t + b^n - w^n/r]/\bar{\alpha}\rangle + \phi^\star(P)/(r\bar{\alpha} \Delta_x) \\
& = \text{arg min}_{P \in \mathbb{R}(\mathcal{T})} \; \frac{1}{2}\| P + A[ (- w^n/r + S^\star[u^n]/\Delta_t + b^n)]/\bar{\alpha} \|^2 + \phi^\star(P)/(r\bar{\alpha} \Delta_x) \end{array}\end{split}\]
where the division has to be understood as a Hadamard product and
\[\bar{\alpha}(t) := \sum_{(x,y) \in S \times S} \alpha(t,x,y)^2.\]
Then \(P^{n+1}\) is given by
\[P^{n+1} = \text{prox}_{\phi^\star/(r\bar{\alpha} \Delta_x)} \left(A[( w^n/r - S^\star[u^n]/\Delta_t - b^n)]/\bar{\alpha}\right).\]
Computation via Moreau’s identity:
Due to the above definition of \(\phi^\star\) and the Moreau identity, we have that
\[ \text{prox}_{\lambda \phi^\star}(x) = x - \lambda\text{prox}_{\lambda^{-1} \phi}(\lambda^{-1}x),\]
for any \(\lambda>0\). In addtion for any \(\xi>0\) we have that
\[\begin{split}\begin{equation}
\text{prox}_{\xi \phi}(x) = \begin{cases} D_{max} & \text{ if } \frac{x - \tau D_0 \bar{D}}{1 + \tau D_0} > D_{max} \\
D_{min} & \text{ if } \frac{x - \tau D_0 \bar{D}}{1 + \tau D_0} < D_{min} \\
\frac{x - \tau D_0 \bar{D}}{1 + \tau D_0} & \text{otherwise}
\end{cases} \end{equation}\end{split}\]
def prox_phi_quad(X,Db,D_0,tau,D_min,D_max):
argmin = (X - tau*D_0*Db)/(1 + tau*D_0)
if argmin > D_max:
argmin = D_max
if argmin < D_min:
argmin = D_min
return(argmin)
def Local_P_prox_quad(u,b,w,n,r,alpha,var_alpha,Db,D_0,D_min,D_max,t):
dt=1/T
dx=1/n
Z = np.zeros((n,n))
for x in range(n):
Z[x] = (w[t,x]/r - u[t+1]/dt - b[t,x])*alpha[t,x]
X = np.sum(Z)/var_alpha[t]
lambde = 1/(r*var_alpha[t]*dx)
new_Pt = X - lambde*prox_phi_quad(X/lambde,Db[t],D_0,1/lambde,D_min,D_max)
return(new_Pt)
def P_argmin_L(u,b,w,T,n,r,alpha,var_alpha,Db,D_0,D_min,D_max):
new_P = np.zeros(T-1)
for t in range(T-1):
new_P[t] = Local_P_prox_quad(u,b,w,n,r,alpha,var_alpha,Db,D_0,D_min,D_max,t)
return new_P
Computation of \(u^{n+1}\)¶
\(u^{n+1}\) is given by
\[\begin{split} \begin{align} u^{n+1} = \text{arg min}_{u \in \mathbb{R}(\bar{\mathcal{T}}\times S)} \langle m^n-\bar{m}_0, (I_0/\Delta_t + I/\Delta_t + I_T)u \rangle_{m} - \langle w^n, S^\star u/\Delta_t \rangle_{w} + \frac{r}{2} \left( \|(I_0/\Delta_t + I/\Delta_t + I_T) u - \gamma^n - \bar{a}^n \|_{m}^2 + \|S^\star u /\Delta_t + A^\star P^{n+1} + b^n \|_{w}^2 \right) \\[2em]
= \text{arg min}_{u \in \mathbb{R}(\bar{\mathcal{T}}\times S)} \langle (I_0\Delta_t + I + I_T) ((m^n-\bar{m}_0)/r - \gamma^n - \bar{a}^n) - S w^n/r + S[A^\star P^{n+1} + b^n], u \rangle_{u} + \frac{1}{2}( \langle (I_0 + I/\Delta_t + I_T) u, u \rangle_{u} +
\langle u, S S^\star u /\Delta_t \rangle_u \end{align}
\end{split}\]
with
\[\begin{split} S S^\star u (t,x) = \begin{cases} 0 & t=0, \\ u(t,x) n & t>0. \end{cases}\end{split}\]
Then
\[\begin{split}u^{n+1}(t) = \begin{cases} ((m^n-\bar{m}_0)/r + \gamma^n + a^n)(t) \Delta_t & t=0, \\
\left( (Sw^n-m^n)/r + \gamma^n + a^n - S[A^\star P^n + b^n] \right)(t)\Delta_t /(1+n) & 0<t<T, \\
\left( (Sw^n-m^n)/r + \gamma^n - S[A^\star P^n + b^n]\right)(t)/(1 +n/\Delta_t) & t = T, \end{cases}\end{split}\]
for any \(t \in \bar{\mathcal{T}}\).
def u_argmin_L(P,gamma,a,b,m,w,m_0,alpha,T,n,r):
dt=1/T
new_u = np.zeros((T,n))
for t in range(T):
for x in range(n):
if t==0:
new_u[t,x] = ((m_0[x] - m[t,x])/r + gamma[t,x] + a[t,x])*dt
elif t==(T-1):
new_u[t,x] = ((-m[t,x] + np.sum(w[t-1,:,x]))/r + gamma[t,x] - np.sum(alpha[t-1,:,x]*P[t-1] + b[t-1,:,x]))/(1+n/dt)
else:
new_u[t,x] = ((-m[t,x] + np.sum(w[t-1,:,x]))/r + gamma[t,x] + a[t,x] - np.sum(alpha[t-1,:,x]*P[t-1] + b[t-1,:,x]))*dt/(1+n)
return new_u
Computation of \(\gamma^{n+1}\)¶
Proximal formulation
\(\gamma^{n+1}\) is given by
\[
\gamma^{n+1} = \text{arg min}_{\gamma \in \mathbb{R}(\bar{\mathcal{T}} \times S)} \frac{1}{2} \|m^n/r + (I_0/\Delta_t + I/\Delta_t + I_T)u^{n+1} - \bar{a}^n - \gamma \|_{m}^2 + \sum_{t \in \mathcal{T}} F^\star[\gamma](t)\Delta_x\Delta_t/r + F^\star[\gamma](T)\Delta_x/r.
\]
\[\begin{split}\gamma^{n+1}(t) = \begin{cases}
\text{prox}_{F^\star/r}\left(m^n/r + u^{n+1}/\Delta_t - \bar{a}^n\right)(t) & t<T, \\
\text{prox}_{F^\star/r}\left(m^n/r + u^{n+1}\right)(t) & t = T. \end{cases}\end{split}\]
for any \(t \in \bar{\mathcal{T}}\).
Computation via Moreau’s identity:
Due to the above definition of \(F^\star\) and the Moreau identity, we have that
\[ \text{prox}_{\lambda F^\star}(x) = x - \lambda\text{prox}_{\lambda^{-1} F}(\lambda^{-1}x),\]
for any \(\lambda>0\). In addtion for any \(\xi>0\) we have that
\[\begin{split}\text{prox}_{\xi F}(x) = \begin{cases} \eta & \text{ if } (x- \xi \nu)/(1+ \xi) > \eta \\
0 & \text{ if } (x- \xi \nu)/(1+ \xi)<0 \\
(x- \xi \nu)/(1+ \xi) &\text{ otherwise } \end{cases}.\end{split}\]
def prox_coeff_F_sharp(X,nu,eta,coeff):
argmin = (X - coeff*nu)/(coeff + 1)
if argmin>eta:
argmin = eta
if argmin<0:
argmin = 0
return(argmin)
def Moreau_id_F(X,nu,eta,lambde):
return(X-lambde*prox_coeff_F_sharp(X/lambde,nu,eta,1/lambde))
def Moreau_gamma_argmin_L(u,a,m,nu,eta,T,n,r):
dt = 1/T
new_gamma = np.zeros((T,n))
for t in range(T):
for x in range(n):
if t == T-1:
X = m[t,x]/r + u[t,x]
new_gamma[t,x] = Moreau_id_F(X,nu[t,x],eta[t,x],1/r)
else:
X = m[t,x]/r + u[t,x]/dt - a[t,x]
new_gamma[t,x] = Moreau_id_F(X,nu[t,x],eta[t,x],1/r)
return(new_gamma)
Computation of \((a^{n+1},b^{n+1})\)¶
\[(a^{n+1},b^{n+1}) = \Pi_{\mathcal{Q}} \big(m^n/r + u^{n+1}/\Delta_t - \gamma^{n+1}, w^n/r - A^\star P^{n+1} - S^\star u^{n+1}/\Delta_t \big).\]
In the linear case, the running cost is given by
\[\ell(t,x,\rho) = \sum_{y\in S} \rho(t,x,y) \beta(t,x,y)\]
with dom\((\ell(t,x,\rho)) = \Delta(S)\). Thus the set \(\mathcal{Q}\) is given by
\[\mathcal{Q} := \left\{ (a,b) \in \mathbb{R}(\mathcal{T} \times S) \times \mathbb{R}(\mathcal{T} \times S \times S) , \; b(t,x,y) - \beta(t,x,y) + a(t,x) \leq 0, \text{ for all } (t,x,y) \in \mathcal{T} \times S \times S \right\}.\]
We define
\[ \bar{a}[m,u,\gamma](t,x) = (m/r + u/\Delta_t - \gamma)(t,x), \qquad \bar{b}[w,P,u](t,x,y) = (w^n/r - A^\star P^{n+1} - S^\star u^{n+1}/\Delta_t)(t,x,y).\]
Then for any \((t,x) \in \mathcal{T} \times S\), we aim at finding
\[(a^{n+1}(t,x),b^{n+1}(t,x,\cdot)) = \Pi_{Q} \big(\bar{a}[m^n,u^{n+1},\gamma^{n+1}](t,x), \bar{b}[w^n,P^{n+1},u^{n+1}](t,x,\cdot) \big)\]
where
\[Q(t,x) := \left\{ (a,b) \in \mathbb{R} \times \mathbb{R}(S) , \; b(y) - \beta(t,x,y) + a \leq 0, \text{ for all } y \in S \right\}.\]
To compute this projection, we define the following minimisation problem
\[\begin{split}\min_{a} \min_{\begin{subarray}{c} b \\ b(y) \leq \beta(y) - a,\text{ for all } y\in S \end{subarray}} (a-\bar{a})^{2}/2 + \sum_{y\in S} (b(y)-\bar{b}(y))^2/2\end{split}\]
The solution to the subproblem
\[\begin{split}\min_{\begin{subarray}{c} b \\ b(y) \leq \beta(y) - a,\text{ for all } y\in S \end{subarray}} (a-\bar{a})^{2}/2 + \sum_{y\in S} (b(y)-\bar{b}(y))^2/2\end{split}\]
is given by
\[b(y) = \min (\bar{b}(y),\beta(y) - a), \quad \text{for all } y \in S.\]
Thus replacing in the initial problem we now need to solve the following optimization problem
\[\min_{a} g(a), \quad g(a) := (a-\bar{a})^{2}/2 + \sum_{y\in S} \max(0,a-\tilde{\beta}(y))^2/2.\]
Let \(\tilde{\beta}(y) := \beta(y)-\bar{b}(y)\). We denote \((y_k)_{k\in \{0,\ldots,n-1\}}\) the sequence such that
\[\tilde{\beta}(y_0) \leq \cdots \leq \tilde{\beta}(y_{n-1}).\]
Then the optimal \(a\) is such that
Optimal a
\[ a = \left(\bar{a} + \sum_{i = 0}^{k-1} \tilde{\beta}(y_i)\right)/(k+1) \]
We have that
\[\partial g(\tilde{\beta}(y_{k})) = (k+1) \tilde{\beta}(y_{k}) - \left(\bar{a} + \sum_{i = 0}^{k-1} \tilde{\beta}(y_i) \right).\]
Then we define the index \(k \in \{1,\ldots,n-1 \}\) if the following conditions are satisfied
\[\begin{equation}
\partial g (\tilde{\beta}(y_{k-1})) < 0, \qquad \partial g (\tilde{\beta}(y_{k})) \geq 0.
\end{equation}\]
Otherwise we set \(k = n\) if \( \partial g (\tilde{\beta}(y_{n-1})) \leq 0\) and \(k = 0\) if \( \partial g (\tilde{\beta}(y_{0})) \geq 0\).
We finally deduce that
Optimal b
\[b(y) = \min \left(\bar{b}(y),\beta(y) - \left(\bar{a} + \sum_{i = 0}^{k-1}\tilde{\beta}(y_i)\right)/(k+1) \right)\]
def proj_Q(a_bar,b_bar,beta,n):
a = 0
b = np.zeros(n)
beta_bar = beta-b_bar
beta_bar_sort = np.sort(beta_bar)
k = 0
sum_beta_bar_sort = 0
derivative_beta = (k+1)*beta_bar_sort[k] - a_bar - sum_beta_bar_sort
while (derivative_beta < 0) and (k < n-1):
sum_beta_bar_sort = sum_beta_bar_sort + beta_bar_sort[k]
k = k+1
derivative_beta = (k+1)*beta_bar_sort[k] - a_bar - sum_beta_bar_sort
if (k==n-1) and (derivative_beta < 0):
sum_beta_bar_sort = sum_beta_bar_sort + beta_bar_sort[k]
k = n
a = (a_bar + sum_beta_bar_sort)/(k+1)
for y in range(n):
b[y] = np.min(np.array([b_bar[y],beta[y] - a]))
return (a,b)
def a_b_proj(P,gamma,u,m,w,T,n,r,alpha,beta):
dt=1/T
(new_a,new_b) = (np.zeros((T-1,n)),np.zeros((T-1,n,n)))
for t in range(T-1):
for x in range(n):
c_1 = m[t,x]/r + u[t,x]/dt - gamma[t,x]
c_3 = w[t,x]/r - alpha[t,x]*P[t] - u[t+1]/dt
(new_a[t,x],new_b[t,x]) = proj_Q(c_1,c_3,beta[t,x],n)
return(new_a,new_b)
#print(proj_Q(np.array([2]),np.array([2,2,-2,5,3]),np.array([0,1,2,3,3]),5))
Computation of \((m^{n+1},w^{n+1})\)¶
We recall that the actualisation of \((m^{n+1},w^{n+1})\) is given by a gradient descent step
\[(m^{n+1},w^{n+1}) = (m^{n},w^{n}) + q((I_0/\Delta_t + I/\Delta_t + I_T)u^{n+1} - \gamma^{n+1} -\bar{a}^{n+1},-A^\star P^{n+1} -S^\star u^{n+1}/\Delta_t - b^{n+1})\]
def m_w_gradient_step(P,gamma,u,a,b,m,w,q,T,n):
dt=1/T
new_m = np.zeros((T,n))
new_w = np.zeros((T-1,n,n))
for t in range(T-1):
for x in range(n):
new_m[t,x] = m[t,x] + q*(u[t,x]/dt - gamma[t,x] - a[t,x])
new_w[t,x] = w[t,x] + q*(- alpha[t,x]*P[t] - u[t+1]/dt - b[t,x])
new_m[T-1] = m[T-1] + q*(u[T-1] - gamma[T-1])
return (new_m,new_w)
Strategy \(\pi = w/m\) and average strategy
def equilibrium_strategy(m,w,T,n,tol=1e-5):
strat = np.zeros((T-1,n,n))
for t in range(T-1):
for x in range(n):
if m[t,x] > tol:
strat[t,x] = w[t,x]/m[t,x]
return(strat)
def mean_field_strategy(pi,T,n):
mfs = np.zeros((T-1,n))
for t in range(T-1):
for x in range(n):
for y in range(n):
mfs[t,x] += pi[t,x,y]*(y-x)
return(mfs)
Reconstruction of \((u,\pi[u])\)
def d_p_mapping(m,w,gamma,P,alpha,beta,T,n,tol = 1e-3,mfg=1):
dt=1/T
dx=1/n
new_u = np.zeros((T,n))
new_pi = np.zeros((T-1,n,n))
f = np.zeros((T,n))
if mfg == 1:
f = gamma
new_u[T-1] = f[T-1]
for t in range(T-1):
for x in range(n):
cost = np.zeros(n)
cost = beta[T-2-t,x]*dt + alpha[T-2-t,x]*P[T-2-t]*dt + new_u[T-1-t]
argmin = np.argmin(cost)
if m[T-2-t,x]*dx>tol:
new_pi[T-2-t,x] = w[T-2-t,x]/m[T-2-t,x]
else:
new_pi[T-2-t,x,argmin] = 1
new_u[T-2-t,x] = cost[argmin] + f[T-2-t,x]*dt
return(new_u,new_pi)
Errors¶
def verification(P,u,gamma,m,pi,w,T,n,beta,nu,m_0,alpha,Db,Dmin,Dmax,eta,mfg = 1):
cost = np.zeros((T-1,n))
Delta_u = np.zeros((T,n))
Delta_pi = np.zeros((T-1,n,n))
Delta_m = np.zeros((T,n))
Delta_gamma = np.zeros((T,n))
Delta_P = np.zeros(T-1)
demand = np.zeros((T-1,n,n))
dt=1/T
dx=1/n
f = np.zeros((T,n))
if mfg == 1:
f = gamma
Delta_m[0] = abs(m[0] - m_0)*dx
for x in range(n):
Delta_u[T-1,x] = abs(u[T-1,x] - f[T-1,x])*dx
for t in range(T-1):
for x in range(n):
arg = beta[t,x]*dt + alpha[t,x]*P[t]*dt + u[t+1]
demand[t,x] = pi[t,x]*m[t,x]*alpha[t,x]*dx
cost[t,x] = np.sum(pi[t,x]*(beta[t,x]*dt + alpha[t,x]*P[t]*dt)) + f[t,x]*dt
Delta_pi[t,x] = abs(np.sum(pi[t,x]*arg) - np.sort(arg)[0])*dx
Delta_m[t+1,x] = abs(m[t+1,x] - np.sum(pi[t,:,x]*m[t]))*dx
Delta_u[t,x] = abs(u[t,x] - cost[t,x] - np.sum(pi[t,x]*u[t+1]))*dx
if gamma[t,x] < nu[t,x]:
Delta_gamma[t,x] = abs(gamma[t,x])*dt*dx
elif gamma[t,x] > eta[t,x] + nu[t,x]:
Delta_gamma[t,x] = abs(gamma[t,x] - eta[t,x])*dt*dx
else:
Delta_gamma[t,x] = abs(gamma[t,x] - m[t,x] - nu[t,x])*dt*dx
D = np.sum(demand[t])
if P[t] > D_0*(Db[t]+Dmax):
Delta_P[t] = abs(P[t]-D_0*(Db[t]+Dmax))*dt
elif P[t] < D_0*(Db[t]+Dmin):
Delta_P[t] = abs(P[t]-D_0*(Db[t]+Dmin))*dt
else:
Delta_P[t] = abs(P[t]- D_0*(Db[t]+D))*dt
return (np.sum(Delta_u),np.sum(Delta_pi),np.sum(Delta_m),np.sum(Delta_P),np.sum(Delta_gamma))
Local transition version¶
tran_0 = np.array([0,1])
tran_interm = np.array([-1,0,1])
tran_n = np.array([-1,0])
def tran(x,n):
if x == 0:
return(tran_0)
if x == n-1:
return(tran_n)
else:
return(tran_interm)
def proj_Q(a_bar,b_bar,beta,n,lenY):
a = 0
b = np.zeros(lenY)
beta_bar = beta-b_bar
beta_bar_sort = np.sort(beta_bar)
k = 0
sum_beta_bar_sort = 0
derivative_beta = (k+1)*beta_bar_sort[k] - a_bar - sum_beta_bar_sort
while (derivative_beta < 0) and (k < lenY-1):
sum_beta_bar_sort = sum_beta_bar_sort + beta_bar_sort[k]
k = k+1
derivative_beta = (k+1)*beta_bar_sort[k] - a_bar - sum_beta_bar_sort
if (k==lenY-1) and (derivative_beta < 0):
sum_beta_bar_sort = sum_beta_bar_sort + beta_bar_sort[k]
k = lenY
a = (a_bar + sum_beta_bar_sort)/(k+1)
for y in range(lenY):
b[y] = np.min(np.array([b_bar[y],beta[y] - a]))
return (a,b)
def a_b_proj(P,gamma,u,m,w,T,n,r,alpha,beta):
dt=1/T
(new_a,new_b) = (np.zeros((T,n)),np.zeros((T-1,n,n)))
for t in range(T-1):
for x in range(n):
Y = tran(x,n) + x
c_1 = m[t,x]/r + u[t,x]/dt - gamma[t,x]
c_3 = w[t,x,Y]/r - alpha[t,x,Y]*P[t] - u[t+1,Y]/dt
(new_a[t,x],new_b[t,x,Y]) = proj_Q(c_1,c_3,beta[t,x,Y],n,len(Y))
return(new_a,new_b)
def u_argmin_L(P,gamma,a,b,m,w,m_0,alpha,T,n,r):
dt=1/T
new_u = np.zeros((T,n))
for t in range(T):
for x in range(n):
Y = tran(x,n) + x
s = len(Y)
if t==0:
new_u[t,x] = ((m_0[x] - m[t,x])/r + gamma[t,x] + a[t,x])*dt
elif t==(T-1):
new_u[t,x] = ((-m[t,x] + np.sum(w[t-1,Y,x]))/r + gamma[t,x] - np.sum(alpha[t-1,Y,x]*P[t-1] + b[t-1,Y,x]))/(1+s/dt)
else:
new_u[t,x] = ((-m[t,x] + np.sum(w[t-1,Y,x]))/r + gamma[t,x] + a[t,x] - np.sum(alpha[t-1,Y,x]*P[t-1] + b[t-1,Y,x]))*dt/(1+s)
return new_u
def alpha_bar(alpha,T,n):
new_alpha = np.zeros((T-1,n))
a = np.zeros(T-1)
for t in range(T-1):
for x in range(n):
Y = tran(x,n) + x
new_alpha[t,x] = np.sum(alpha[t,x,Y]**2)
a[t] = np.sum(new_alpha[t])
return(a)
def Local_P_prox_quad(u,b,w,n,r,alpha,var_alpha,Db,D_0,D_min,D_max,t):
dt=1/T
dx=1/n
Z = np.zeros((n,n))
for x in range(n):
Y = tran(x,n) + x
Z[x,Y] = (w[t,x,Y]/r - u[t+1,Y]/dt - b[t,x,Y])*alpha[t,x,Y]
X = np.sum(Z)/var_alpha[t]
lambde = 1/(r*var_alpha[t]*dx)
new_Pt = X - lambde*prox_phi_quad(X/lambde,Db[t],D_0,1/lambde,D_min,D_max)
return(new_Pt)
def m_w_gradient_step(P,gamma,u,a,b,m,w,q,T,n):
dt=1/T
new_m = np.zeros((T,n))
new_w = np.zeros((T-1,n,n))
for t in range(T-1):
for x in range(n):
Y = tran(x,n) + x
new_m[t,x] = m[t,x] + q*(u[t,x]/dt - gamma[t,x] - a[t,x])
new_w[t,x,Y] = w[t,x,Y] + q*(- alpha[t,x,Y]*P[t] - u[t+1,Y]/dt - b[t,x,Y])
new_m[T-1] = m[T-1] + q*(u[T-1] - gamma[T-1])
return (new_m,new_w)
def equilibrium_strategy(m,w,T,n,tol=1e-5):
strat = np.zeros((T-1,n,n))
for t in range(T-1):
for x in range(n):
Y = tran(x,n) + x
if m[t,x] > tol:
strat[t,x,Y] = w[t,x,Y]/m[t,x]
return(strat)
def d_p_mapping(m,w,gamma,P,alpha,beta,T,n,tol = 1e-3,mfg=1):
dt=1/T
dx=1/n
new_u = np.zeros((T,n))
new_pi = np.zeros((T-1,n,n))
f = np.zeros((T,n))
if mfg == 1:
f = gamma
new_u[T-1] = f[T-1]
for t in range(T-1):
for x in range(n):
cost = np.zeros(n)
Y = tran(x,n) + x
cost[Y] = beta[T-2-t,x,Y]*dt + alpha[T-2-t,x,Y]*P[T-2-t]*dt + new_u[T-1-t,Y]
argmin = np.argmin(cost[Y])
if m[T-2-t,x]*dx>tol:
new_pi[T-2-t,x,Y] = w[T-2-t,x,Y]/m[T-2-t,x]
else:
new_pi[T-2-t,x,Y[argmin]] = 1
new_u[T-2-t,x] = cost[Y[argmin]] + f[T-2-t,x]*dt
return(new_u,new_pi)
def verification(P,u,gamma,m,pi,w,T,n,beta,nu,m_0,alpha,Db,Dmin,Dmax,eta,mfg = 1):
cost = np.zeros((T-1,n))
Delta_u = np.zeros((T,n))
Delta_pi = np.zeros((T-1,n,n))
Delta_m = np.zeros((T,n))
Delta_gamma = np.zeros((T,n))
Delta_P = np.zeros(T-1)
demand = np.zeros((T-1,n,n))
dt=1/T
dx=1/n
f = np.zeros((T,n))
if mfg == 1:
f = gamma
Delta_m[0] = abs(m[0] - m_0)*dx
for x in range(n):
Delta_u[T-1,x] = abs(u[T-1,x] - f[T-1,x])*dx
for t in range(T-1):
for x in range(n):
Y = tran(x,n) + x
arg = beta[t,x,Y]*dt + alpha[t,x,Y]*P[t]*dt + u[t+1,Y]
demand[t,x,Y] = pi[t,x,Y]*m[t,x]*alpha[t,x,Y]*dx
cost[t,x] = np.sum(pi[t,x,Y]*(beta[t,x,Y]*dt + alpha[t,x,Y]*P[t]*dt)) + f[t,x]*dt
Delta_pi[t,x] = abs(np.sum(pi[t,x,Y]*arg) - np.sort(arg)[0])*dx
Delta_m[t+1,x] = abs(m[t+1,x] - np.sum(pi[t,Y,x]*m[t,Y]))*dx
Delta_u[t,x] = abs(u[t,x] - cost[t,x] - np.sum(pi[t,x,Y]*u[t+1,Y]))*dx
if gamma[t,x] < 0:
Delta_gamma[t,x] = abs(m[t,x])*dt*dx
elif gamma[t,x] > eta[t,x] + nu[t,x]:
Delta_gamma[t,x] = abs(m[t,x] - eta[t,x])*dt*dx
else:
Delta_gamma[t,x] = abs(gamma[t,x] - m[t,x])*dt*dx
D = np.sum(demand[t])
if P[t] > D_0*(Db[t]+Dmax):
Delta_P[t] = abs(D-Dmax)*dt
elif P[t] < D_0*(Db[t]+Dmin):
Delta_P[t] = abs(D-Dmin)*dt
else:
Delta_P[t] = abs(D- (P[t]/D_0 - Db[t]))*dt
return (np.sum(Delta_u),np.sum(Delta_pi),np.sum(Delta_m),np.sum(Delta_P),np.sum(Delta_gamma))
ADMM¶
MFG¶
T = 50
n = T
alpha = np.zeros((T-1,n,n))
r = 2/n
q = r
var_alpha = alpha_bar(alpha,T,n)
m_0 = initial_mass(n)
beta = displacement_cost(T,n)
nu = np.zeros((T,n))
eta = sharp_penalisation_congestion(T,n)
Dmin = -10
Dmax = 10
D_0 = 1/2
Db = reference_demand(T)*0
P = np.zeros(T-1)
var_P = P
u = np.random.rand(T,n)
gamma = np.zeros((T,n))
m = np.random.rand(T,n) + 1
w = np.zeros((T-1,n,n)) + 1
(a,b) = (m,w)
N = 10000
start = time.time()
error = np.zeros(N)
mfg_error = np.zeros((N,5))
ev_m_s = np.zeros((N,T-1,n))
ev_m = np.zeros((N,T,n))
ev_u = np.zeros((N,T,n))
for i in range(N):
print(round(i/N*100, 2)," \r",end = '')
var_u = u_argmin_L(var_P,gamma,a,b,m,w,m_0,alpha,T,n,r)
var_gamma = Moreau_gamma_argmin_L(var_u,a,m,nu,eta,T,n,r)
(var_a,var_b) = a_b_proj(var_P,var_gamma,var_u,m,w,T,n,r,alpha,beta)
(var_m,var_w) = m_w_gradient_step(var_P,var_gamma,var_u,var_a,var_b,m,w,q,T,n)
(u,gamma,a,b,m,w) = (var_u,var_gamma,var_a,var_b,var_m,var_w)
(U,Pi) = d_p_mapping(m,w,gamma,P,alpha,beta,T,n,tol = 1e-4)
mfg_error[i] = np.array(verification(P,U,gamma,m,Pi,w,T,n,beta,nu,m_0,alpha,Db,Dmin,Dmax,eta))
(ev_m_s[i],ev_m[i],ev_u[i]) = (mean_field_strategy(Pi,T,n),m,U)
end = time.time()
print("\n execution time :",round(end-start,2), "s")
99.99
execution time : 5304.06 s
#plt.plot(np.log(mfg_error[:,0])/np.log(10), label = r'$\log(||\varepsilon_u||_1)$', color = 'blue')
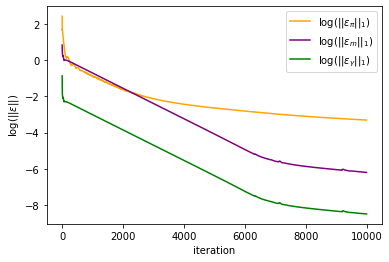
plt.plot(np.log(mfg_error[:,1])/np.log(10), label = r'$\log(||\varepsilon_\pi||_1)$', color = 'orange')
plt.plot(np.log(mfg_error[:,2])/np.log(10), label = r'$\log(||\varepsilon_m||_1)$', color = 'purple')
plt.plot(np.log(mfg_error[:,4])/np.log(10), label = r'$\log(||\varepsilon_{\gamma}||_1)$', color = 'green')
#plt.plot(np.log(mfg_error[:,3])/np.log(10), label = r'$\log(||\varepsilon_P||_1)$', color = 'red')
plt.xlabel('iteration')
plt.ylabel(r'$\log(||\varepsilon||)$')
plt.legend()
plt.savefig('ADMM_constraint_mfg_error.png', dpi=500, bbox_inches='tight')
t = np.linspace(0, 1, T)
y = np.linspace(0, 1, n)
X, Y = np.meshgrid(y, t)
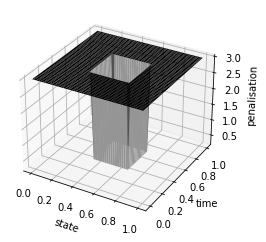
Z = eta
fig = plt.figure()
ax = plt.axes(projection='3d')
#ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='Greys', edgecolor='none')
#ax.plot_wireframe(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
ax.set_xlabel('state')
ax.set_ylabel('time')
ax.set_zlabel('penalisation')
plt.savefig('eta.png', dpi=500, bbox_inches='tight')
#%matplotlib notebook
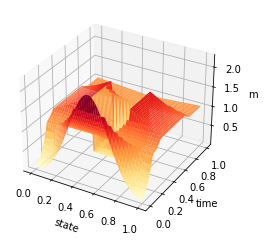
Z = m
fig = plt.figure()
ax = plt.axes(projection='3d')
#ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='YlOrRd', edgecolor='none')
#ax.plot_wireframe(X, Y, Z, rstride=1, cstride=1, cmap='v£iridis', edgecolor='none')
ax.set_xlabel('state')
ax.set_ylabel('time')
ax.set_zlabel('m')
plt.savefig('ADMM_constraint_mfg_m.png', dpi=500, bbox_inches='tight')
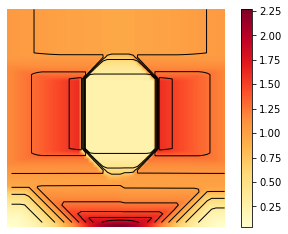
X, Y = np.meshgrid(t, y)
Z = m
minm = np.min(Z)
maxm = np.max(Z)
levels = np.linspace(minm,maxm,10)
fig, ax = plt.subplots()
im = ax.imshow(Z, interpolation='bilinear', origin='lower',
cmap='YlOrRd')
plt.axis('off')
CS = ax.contour(Z,levels, origin='lower', colors='black',
linewidths=1)
CBI = fig.colorbar(im)
plt.savefig('ADMM_constraint_mfg_m_contour.png', dpi=500, bbox_inches='tight')
t = np.linspace(0, 1, T)
y = np.linspace(0, 1, n)
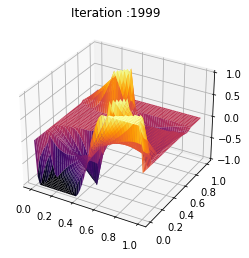
Nb_im = 2000
X, Y = np.meshgrid(y, t)
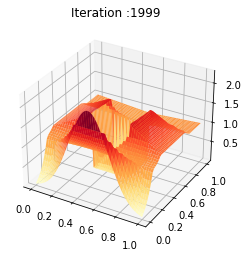
Z = ev_m[:Nb_im]
def update_plot(frame_number, zarray, plot):
plot[0].remove()
plt.title('Iteration :%s'%frame_number)
plot[0] = ax.plot_surface(X, Y, Z[frame_number,:,:], cmap="YlOrRd",edgecolor='none')
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
fps = 100
plot = [ax.plot_surface(X, Y, Z[0,:,:], rstride=1, cstride=1)]
ani = animation.FuncAnimation(fig, update_plot, Nb_im, fargs=(Z, plot), interval=2000/fps)
ani.save('ADMM_constraint_mfg_m_convergence.mp4',writer='ffmpeg',fps=fps)
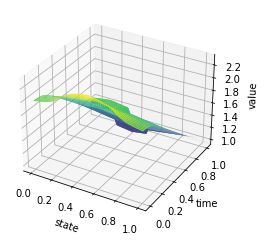
Z = U
fig = plt.figure()
ax = plt.axes(projection='3d')
#ax.contour3D(X, Y, Z, 50, cmap='magma')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
#ax.plot_wireframe(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
ax.set_xlabel('state')
ax.set_ylabel('time')
ax.set_zlabel('value')
plt.savefig('ADMM_constraint_mfg_u.png', dpi=500, bbox_inches='tight')
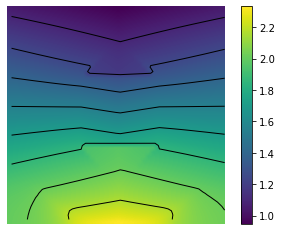
X, Y = np.meshgrid(t, y)
Z = U
minu = np.min(Z)
maxu = np.max(Z)
levels = np.linspace(minu,maxu,10)
fig, ax = plt.subplots()
im = ax.imshow(Z, interpolation='bilinear', origin='lower',
cmap='viridis')
plt.axis('off')
CS = ax.contour(Z,levels, origin='lower', colors='black',
linewidths=1)
CBI = fig.colorbar(im)
plt.savefig('ADMM_constraint_mfg_u_contour.png', dpi=500, bbox_inches='tight')
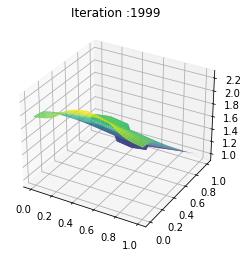
t = np.linspace(0, 1, T)
y = np.linspace(0, 1, n)
Nb_im = 2000
X, Y = np.meshgrid(y, t)
Z = ev_u[:Nb_im]
def update_plot(frame_number, zarray, plot):
plot[0].remove()
plt.title('Iteration :%s'%frame_number)
plot[0] = ax.plot_surface(X, Y, Z[frame_number,:,:], cmap="viridis",edgecolor='none')
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
fps = 100
plot = [ax.plot_surface(X, Y, Z[0,:,:], rstride=1, cstride=1)]
ani = animation.FuncAnimation(fig, update_plot, Nb_im, fargs=(Z, plot), interval=2000/fps)
ani.save('ADMM_constraint_mfg_u_convergence.mp4',writer='ffmpeg',fps=fps)
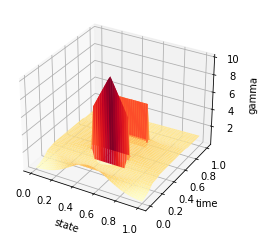
Z = gamma
fig = plt.figure()
ax = plt.axes(projection='3d')
#ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='YlOrRd', edgecolor='none')
#ax.plot_wireframe(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
ax.set_xlabel('state')
ax.set_ylabel('time')
ax.set_zlabel('gamma')
plt.savefig('ADMM_constraint_mfg_gamma.png', dpi=500, bbox_inches='tight')
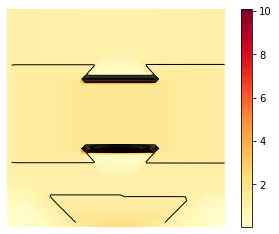
X, Y = np.meshgrid(t, y)
Z = gamma
minu = np.min(Z)
maxu = np.max(Z)
levels = np.linspace(minu,maxu,10)
fig, ax = plt.subplots()
im = ax.imshow(Z, interpolation='bilinear', origin='lower',
cmap='YlOrRd')
plt.axis('off')
CS = ax.contour(Z,levels, origin='lower', colors='black',
linewidths=1)
CBI = fig.colorbar(im)
plt.savefig('ADMM_constraint_mfg_gamma_contour.png', dpi=500, bbox_inches='tight')
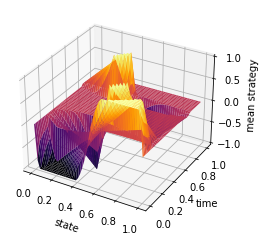
ti = np.linspace(0, 1, T-1)
y = np.linspace(0, 1, n)
X, Y = np.meshgrid(y, ti)
Z = mean_field_strategy(Pi,T,n)
fig = plt.figure()
ax = plt.axes(projection='3d')
#ax.contour3D(X, Y, Z, 50, cmap='magma')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='inferno', edgecolor='none')
#ax.plot_wireframe(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
ax.set_xlabel('state')
ax.set_ylabel('time')
ax.set_zlabel('mean strategy')
plt.savefig('ADMM_constraint_mfg_mean_strategy.png', dpi=500, bbox_inches='tight')
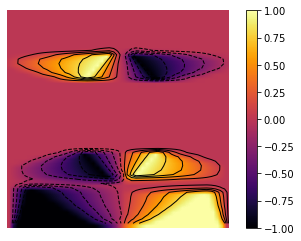
minm = np.min(Z)
maxm = np.max(Z)
levels = np.linspace(minm,maxm,10)
fig, ax = plt.subplots()
im = ax.imshow(Z, interpolation='bilinear', origin='lower',
cmap='inferno')
plt.axis('off')
CS = ax.contour(Z,levels, origin='lower', colors='black',
linewidths=1)
CBI = fig.colorbar(im)
plt.savefig('ADMM_constraint_mfg_mean_strategy_contour.png', dpi=500, bbox_inches='tight')
ti = np.linspace(0, 1, T-1)
y = np.linspace(0, 1, n)
Nb_im = 2000
X, Y = np.meshgrid(y, ti)
Z = ev_m_s[:Nb_im]
def update_plot(frame_number, zarray, plot):
plot[0].remove()
plt.title('Iteration :%s'%frame_number)
plot[0] = ax.plot_surface(X, Y, Z[frame_number,:,:], cmap="inferno",edgecolor='none')
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
fps = 100
plot = [ax.plot_surface(X, Y, Z[0,:,:], rstride=1, cstride=1)]
ani = animation.FuncAnimation(fig, update_plot, Nb_im, fargs=(Z, plot), interval=2000/fps)
ani.save('ADMM_constraint_mfg_mean_strategy_convergence.mp4',writer='ffmpeg',fps=fps)
MFGC¶
T = 50
n = T
alpha = alpha_cost(T,n)
r = 1/2
q = r
var_alpha = alpha_bar(alpha,T,n)
m_0 = initial_mass(n)
beta = displacement_cost(T,n)
nu = np.zeros((T,n))
D_0 = 1/2
Db = reference_demand(T)*2
Dmin = -2
Dmax = 0
P = np.zeros(T-1)
u = np.random.rand(T,n)
gamma = np.zeros((T,n))
var_gamma = gamma
m = np.random.rand(T,n)
w = np.zeros((T-1,n,n)) + 1
(a,b) = (m,w)
N = 10000
start = time.time()
error = np.zeros(N)
ev_m_s = np.zeros((N,T-1,n))
ev_m = np.zeros((N,T,n))
ev_u = np.zeros((N,T,n))
mfg_error = np.zeros((N,5))
for i in range(N):
print(round(i/N*100, 2)," \r",end = '')
var_P = P_argmin_L(u,b,w,T,n,r,alpha,var_alpha,Db,D_0,Dmin,Dmax)
var_u = u_argmin_L(var_P,gamma,a,b,m,w,m_0,alpha,T,n,r)
(var_a,var_b) = a_b_proj(var_P,var_gamma,var_u,m,w,T,n,r,alpha,beta)
(var_m,var_w) = m_w_gradient_step(var_P,var_gamma,var_u,var_a,var_b,m,w,q,T,n)
(P,u,a,b,m,w) = (var_P,var_u,var_a,var_b,var_m,var_w)
(U,Pi) = d_p_mapping(m,w,gamma,P,alpha,beta,T,n,tol = 1e-4)
mfg_error[i] = np.array(verification(P,U,gamma,m,Pi,w,T,n,beta,nu,m_0,alpha,Db,Dmin,Dmax,eta,mfg=0))
(ev_m_s[i],ev_m[i],ev_u[i]) = (mean_field_strategy(Pi,T,n),m,U)
end = time.time()
print("\n execution time :",round(end-start,2), "s")
99.99
execution time : 4797.56 s
#plt.plot(np.log(mfg_error[:,0])/np.log(10), label = r'$\log(||\varepsilon_u||_1)$', color = 'blue')
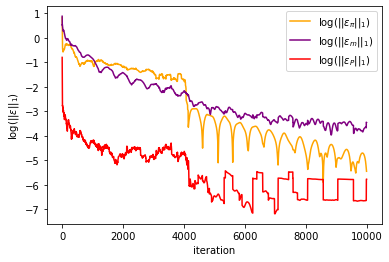
plt.plot(np.log(mfg_error[:,1])/np.log(10), label = r'$\log(||\varepsilon_\pi||_1)$', color = 'orange')
plt.plot(np.log(mfg_error[:,2])/np.log(10), label = r'$\log(||\varepsilon_m||_1)$', color = 'purple')
#plt.plot(np.log(mfg_error[:,4])/np.log(10), label = r'$\log(||\varepsilon_{\gamma}||_1)$', color = 'green')
plt.plot(np.log(mfg_error[:,3])/np.log(10), label = r'$\log(||\varepsilon_P||_1)$', color = 'red')
plt.xlabel('iteration')
plt.ylabel(r'$\log(||\varepsilon||_1)$')
plt.legend()
plt.savefig('ADMM_constraint_mfgc_error.png', dpi=500, bbox_inches='tight')
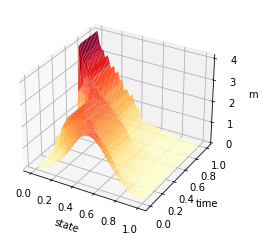
t = np.linspace(0, 1, T)
y = np.linspace(0, 1, n)
X, Y = np.meshgrid(t, y)
Z = m
fig = plt.figure()
ax = plt.axes(projection='3d')
#ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='YlOrRd', edgecolor='none')
#ax.plot_wireframe(X, Y, Z, rstride=1, cstride=1, cmap='v£iridis', edgecolor='none')
ax.set_xlabel('state')
ax.set_ylabel('time')
ax.set_zlabel('m')
plt.savefig('ADMM_constraint_mfgc_m.png', dpi=500, bbox_inches='tight')
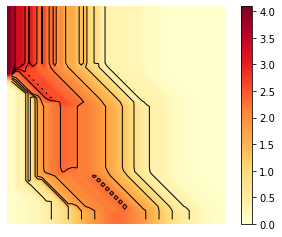
Z = m
minm = np.min(Z)
maxm = np.max(Z)
levels = np.linspace(minm,maxm,10)
fig, ax = plt.subplots()
im = ax.imshow(Z, interpolation='bilinear', origin='lower',
cmap='YlOrRd')
plt.axis('off')
CS = ax.contour(Z,levels, origin='lower', colors='black',
linewidths=1)
CBI = fig.colorbar(im)
plt.savefig('ADMM_constraint_mfgc_m_contour.png', dpi=500, bbox_inches='tight')
t = np.linspace(0, 1, T)
y = np.linspace(0, 1, n)
Nb_im = 2000
X, Y = np.meshgrid(y, t)
Z = ev_m[:Nb_im]
def update_plot(frame_number, zarray, plot):
plot[0].remove()
plt.title('Iteration :%s'%frame_number)
plot[0] = ax.plot_surface(X, Y, Z[frame_number,:,:], cmap="YlOrRd",edgecolor='none')
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
fps = 100
plot = [ax.plot_surface(X, Y, Z[0,:,:], rstride=1, cstride=1)]
ani = animation.FuncAnimation(fig, update_plot, Nb_im, fargs=(Z, plot), interval=2000/fps)
ani.save('ADMM_constraint_mfgc_m_convergence.mp4',writer='ffmpeg',fps=fps)
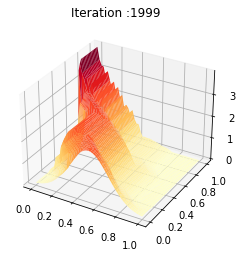
Z = U
fig = plt.figure()
ax = plt.axes(projection='3d')
#ax.contour3D(X, Y, Z, 50, cmap='magma')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
#ax.plot_wireframe(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
ax.set_xlabel('state')
ax.set_ylabel('time')
ax.set_zlabel('value')
plt.savefig('ADMM_constraint_mfgc_u.png', dpi=500, bbox_inches='tight')
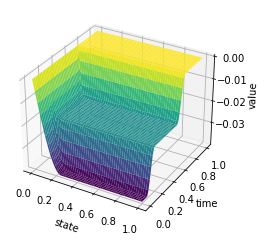
X, Y = np.meshgrid(t, y)
Z = U
minu = np.min(Z)
maxu = np.max(Z)
levels = np.linspace(minu,maxu,10)
fig, ax = plt.subplots()
im = ax.imshow(Z, interpolation='bilinear', origin='lower',
cmap='viridis')
plt.axis('off')
CS = ax.contour(Z,levels, origin='lower', colors='black',
linewidths=1)
CBI = fig.colorbar(im)
plt.savefig('ADMM_constraint_mfgc_u_contour.png', dpi=500, bbox_inches='tight')
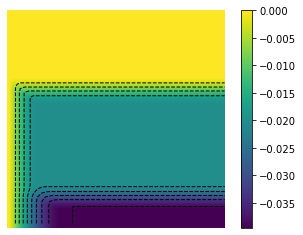
t = np.linspace(0, 1, T)
y = np.linspace(0, 1, n)
Nb_im = 2000
X, Y = np.meshgrid(y, t)
Z = ev_u[:Nb_im]
def update_plot(frame_number, zarray, plot):
plot[0].remove()
plt.title('Iteration :%s'%frame_number)
plot[0] = ax.plot_surface(X, Y, Z[frame_number,:,:], cmap="viridis",edgecolor='none')
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
fps = 100
plot = [ax.plot_surface(X, Y, Z[0,:,:], rstride=1, cstride=1)]
ani = animation.FuncAnimation(fig, update_plot, Nb_im, fargs=(Z, plot), interval=2000/fps)
ani.save('ADMM_constraint_mfgc_u_convergence.mp4',writer='ffmpeg',fps=fps)
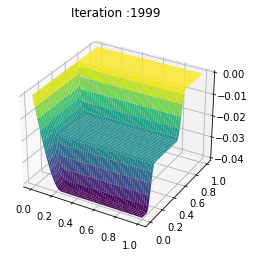
ti = np.linspace(0, 1, T-1)
y = np.linspace(0, 1, n)
X, Y = np.meshgrid(y, ti)
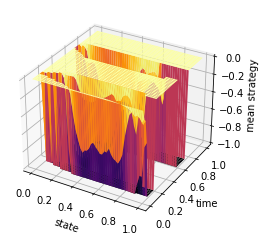
Z = mean_field_strategy(Pi,T,n)
fig = plt.figure()
ax = plt.axes(projection='3d')
#ax.contour3D(X, Y, Z, 50, cmap='magma')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='inferno', edgecolor='none')
#ax.plot_wireframe(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
ax.set_xlabel('state')
ax.set_ylabel('time')
ax.set_zlabel('mean strategy')
plt.savefig('ADMM_constraint_mfgc_mean_strategy.png', dpi=500, bbox_inches='tight')
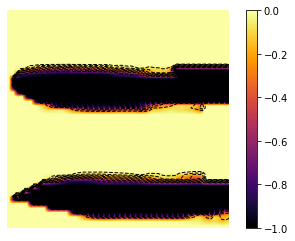
minm = np.min(Z)
maxm = np.max(Z)
levels = np.linspace(minm,maxm,10)
fig, ax = plt.subplots()
im = ax.imshow(Z, interpolation='bilinear', origin='lower',
cmap='inferno')
plt.axis('off')
CS = ax.contour(Z,levels, origin='lower', colors='black',
linewidths=1)
CBI = fig.colorbar(im)
plt.savefig('ADMM_constraint_mfgc_mean_strategy_contour.png', dpi=500, bbox_inches='tight')
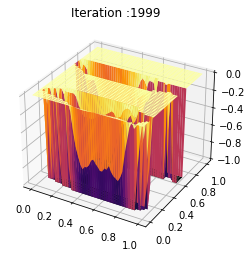
ti = np.linspace(0, 1, T-1)
y = np.linspace(0, 1, n)
Nb_im = 2000
X, Y = np.meshgrid(y, ti)
Z = ev_m_s[:Nb_im]
def update_plot(frame_number, zarray, plot):
plot[0].remove()
plt.title('Iteration :%s'%frame_number)
plot[0] = ax.plot_surface(X, Y, Z[frame_number,:,:], cmap="inferno",edgecolor='none')
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
fps = 100
plot = [ax.plot_surface(X, Y, Z[0,:,:], rstride=1, cstride=1)]
ani = animation.FuncAnimation(fig, update_plot, Nb_im, fargs=(Z, plot), interval=2000/fps)
ani.save('ADMM_constraint_mfgc_mean_strategy_convergence.mp4',writer='ffmpeg',fps=fps)
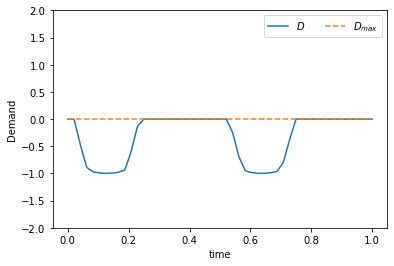
def demand(Db,D_0,alpha,w,T,n):
dx=1/n
D_eff = np.zeros(T-1)
for t in range(T-1):
D_eff[t] = (np.sum(alpha[t]*w[t])*dx)
return(D_eff)
plt.plot(np.linspace(0,1,T-1),demand(Db,D_0,alpha,w,T,n), '-',label=r'$D$')
plt.plot(np.linspace(0,1,T-1),np.zeros(T-1) + Dmax,'--', label = r'$D_{max}$')
plt.legend(loc='upper right',
ncol=2)
plt.xlabel('time')
plt.ylabel('Demand')
plt.ylim([-2, 2])
plt.savefig('Dbar_Dmin.png', dpi=500, bbox_inches='tight')
def real_demand(Db,D_0,alpha,w,T,n):
dx=1/n
D_eff = np.zeros(T-1)
for t in range(T-1):
D_eff[t] = (np.sum(alpha[t]*w[t])*dx + Db[t])
return(D_eff)
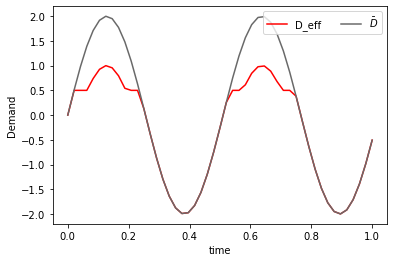
plt.plot(np.linspace(0,1,T-1),real_demand(Db,D_0,alpha,w,T,n), 'r-',label='D_eff')
plt.plot(np.linspace(0,1,T-1),Db, color = 'dimgrey', label = r'$\bar{D}$')
plt.legend(loc='upper right',
ncol=2)
plt.xlabel('time')
plt.ylabel('Demand')
plt.savefig('ADMM_constraint_mfgc_D.png', dpi=500, bbox_inches='tight')
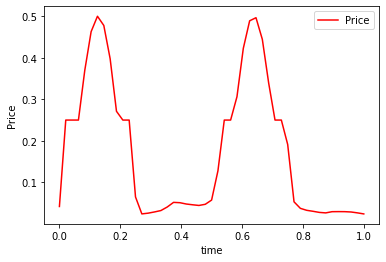
plt.plot(np.linspace(0,1,T-1),P, 'r-',label='Price')
plt.legend(loc='upper right',
ncol=2)
plt.xlabel('time')
plt.ylabel('Price')
plt.savefig('ADMM_constraint_mfgc_P.png', dpi=500, bbox_inches='tight')
- BB00
Jean-David Benamou and Yann Brenier. A computational fluid mechanics solution to the monge-kantorovich mass transfer problem. Numerische Mathematik, 84(3):375–393, 2000.